Граф (від грецького «графо», що пишу, креслю, малюю) — це множина точок (вершин графа), деякі з яких сполучені лініями (ребрами графа). При цьому пара вершин може сполучатися декількома ребрами.

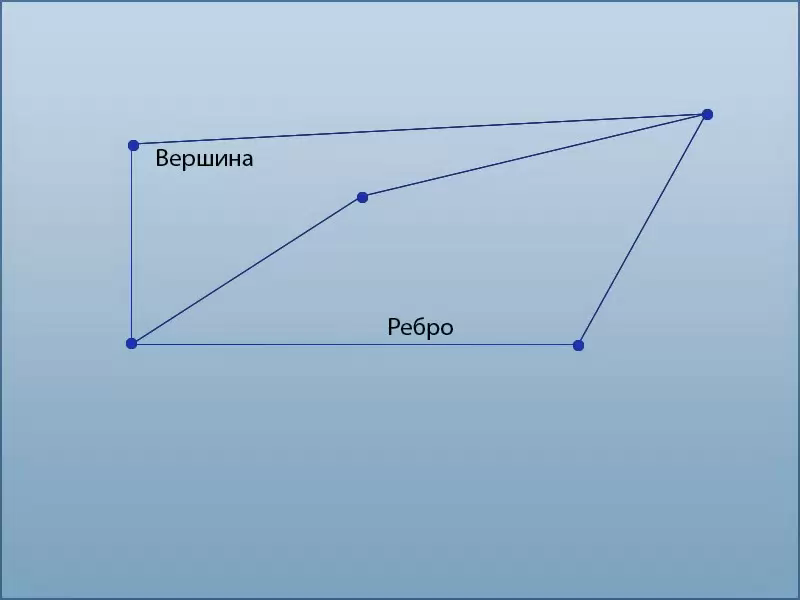
 мал.1

        Прикладами графів є карти автомобільних  доріг  чи залізниць, схеми метрополітенів, генеалогічні дерева.

 

 

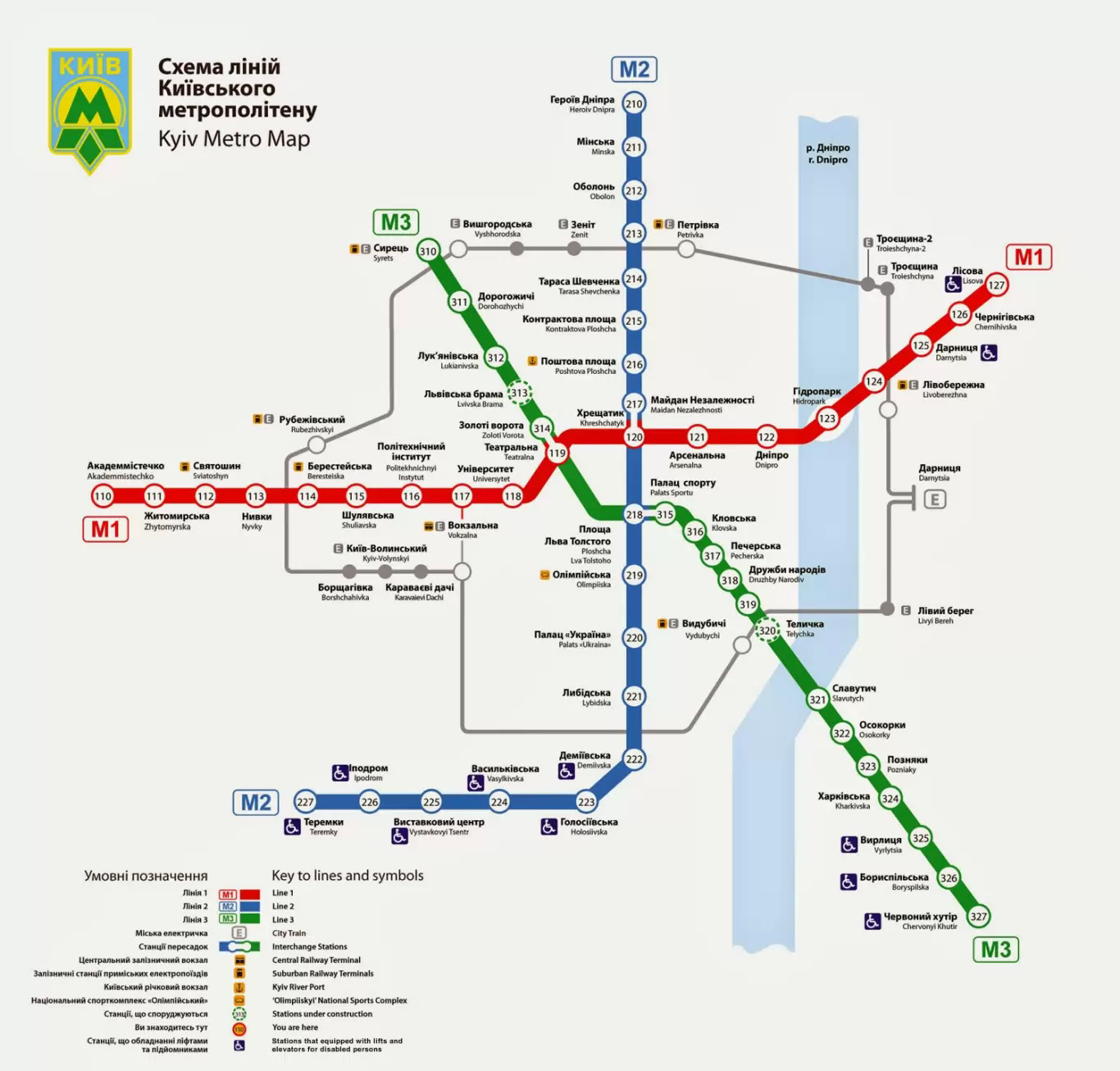
мал.2

          Перша робота з теорії графів належить Леонардові Ейлеру. Вона була створена 1736 року. Розпочиналася ця робота з розглядання задачі про кенігсберзькі мости.   Видатний  математик народився у Швейцарії. На запрошення Петербурзької академії наук 1727 року він переїхав до Росії. Наукова спадщина Ейлера вражає своїм обсягом і різнобічністю. У списку його праць понад 880 назв. Останні 17 років його життя було затьмарене майже повною втратою зору. Але він продовжував творити, як і в молоді роки. Для багатьох поколінь математиків Ейлер був учителем. Матеріали його досліджень увійшли до сучасних підручників із вищої математики.

 мал. 3

 

 ЗАДАЧА ПРО КЕНІГСБЕРЗЬКІ МОСТИ

          Місто  Кенігсберг (нині Калінінград) розташоване на берегах і двох островах річки Преголі. Різні частини міста були сполучені мостами, як показано на рисунку. Щонеділі мешканці прогулювалися містом і цікавилися питанням: чи можна вибрати такий маршрут, щоб пройти кожним мостом тільки один раз і повернутися до початкової точки?

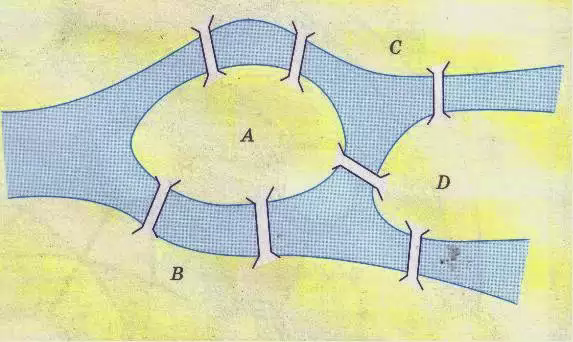
 мал. 4

 

ПОДУМАЙ І РОЗВ’ЯЖИ!

 Задача І. «Сварливі сусіди»

        Мешканці п'яти будинків посварилися між собою і, щоб не зустрічатися біля колодязів, вирішили поділити їх так, щоб господар кожного будинку ходив «своєю» стежкою до «свого» колодязя. Чи можливо це зробити, якщо будинки і колодязі розташовані так, як показано на рисунку?

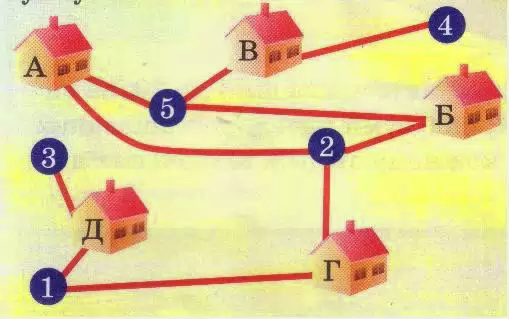
 мал. 5

 Задача ІІ. «Не відриваючи олівця від паперу»

          Не відриваючи олівця від паперу і не проводячи по жодному з ребер двічі, побудуйте граф, зображений на рисунку. Занумеруйте ребра в тій послідовності, в якій ви їх проходили.

Мал. 6